HeroCTF v6 - Interpolation

Description

Write Up: Tyron
Créateur: alol
Difficulté: facile
Points: 200
Format du flag: Hero{printable}

Enoncé

Français: Des données manquantes ont-elles vraiment stoppé quelqu'un ?
English: Has missing data really stopped anyone ?

Pièce(s) jointe(s):

sources

Solution détaillée

On a un serveur qui crée un polynome à partir du flag coupé en plusieurs parties puis hashé. Il calcule des points avec ce polynome et nous les envoie.

Lecture du code source

#!/usr/bin/sage
import hashlib
import re

with open("flag.txt", "rb") as f:
    FLAG = f.read()
    assert re.match(rb"Hero{[0-9a-zA-Z_]{90}}", FLAG)

F = FiniteField(2**256 - 189)
R = PolynomialRing(F, "x")
H = lambda n: int(hashlib.sha256(n).hexdigest(), 16)
C = lambda x: [H(x[i : i + 4]) for i in range(0, len(FLAG), 4)]

f = R(C(FLAG))

points = []
for _ in range(f.degree()):
    r = F.random_element()
    points.append([r, f(r)])
print(points)

flag = input(">").encode().ljust(len(FLAG))

g = R(C(flag))

for p in points:
    if g(p[0]) != p[1]:
        print("Wrong flag!")
        break
else:
    print("Congrats!")

Ici assert re.match(rb"Hero{[0-9a-zA-Z_]{90}}", FLAG), on connait les caractères utilisés pour le flag, leur nombre de 90, et ajouté à cela Hero{}, le flag fait 96 caractères.

Un corps fini est défini : F = FiniteField(2**256 - 189) aussi noté ZnZ avec $ n = 2^{256} -189 $. C'est une notion d'arithmétique modulaire qui implique de tous les nombres avec lesquels ont travaille sont modulo n. Il y a un module cryptohack qui aborde ces notions.

Ensuite, on initialise un objet polynome dans le corps fini F : R = PolynomialRing(F, "x"). Il est basé sur une unique variable x alors on appelle ça un polynome univarié.

Une fonction H qui ne fait que hacher des octets donnés et la fonction C vient séparer une chaine de caractère en morceau de 4 octets, hache chacun d'entre eux avec H et les ajoute dans une liste.

H = lambda n: int(hashlib.sha256(n).hexdigest(), 16)
C = lambda x: [H(x[i : i + 4]) for i in range(0, len(FLAG), 4)]

Ensuite le polynome est généré avec : f = R(C(FLAG)).

D'ailleurs un polynome P s'écrit:

\[ P(X) = a_{n}X^{n} + a_{n-1}X^{n-1} + \ ... \ + a_{2}X^{2} + a_{1}X^{1} + a_{0} \]

En gros, ce qu'on voyait au lycée c'est un polynome : $$ ax^{2} + bx +c $$ On l'appelle polynome du second degré, car le degré d'un polynome est le plus grand entier i tel que $ a_{i} \neq 0 $.

Et les coefficients sont les valeurs a du polynome P.

Il y a n nombre x aléatoires générés, leurs image y est calculée à travers le polynome et le couple [x,y] est ajouté dans la liste points. Et cette liste de points nous est révelée.

points = []
for _ in range(f.degree()):
    r = F.random_element()
    points.append([r, f(r)])
print(points)

Ensuite une entrée utilisateur est demandée, et un polynome sera généré comme il l'a été avec le FLAG et les résultats obtenus avec notre entrée sera comparé avec les résultats obtenus avec le FLAG.

g = R(C(flag))

for p in points:
    if g(p[0]) != p[1]:
        print("Wrong flag!")
        break
else:
    print("Congrats!")

Le FLAG ne sera pas affiché à l'issue de notre entrée utilisateur donc, on est censé pouvoir retrouver le flag de notre coté.

Vulnérabilités

Le chemin logique pour moi est que, à partir des points et leur images envoyées par le serveur, reconstruire le polynome. Récupérer les coefficients du polynome et ensuite de remonter jusqu'à la valeur de chaque coeffs avant d'etre hachés. C'est une sorte de bruteforce et je vais utiliser une rainbow table pour ça.

Reconstruction du polynome

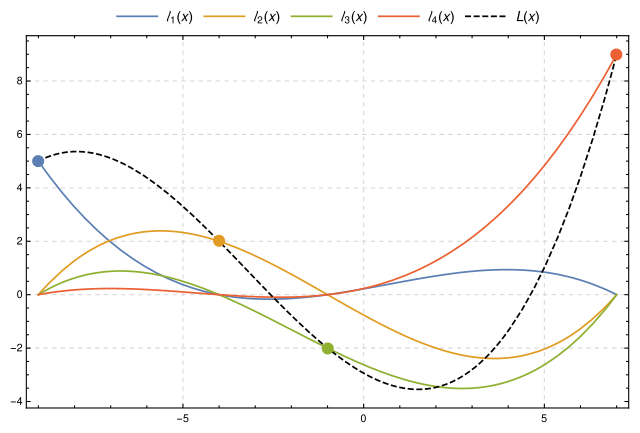
Il faut savoir que un polynome peut etre reconstruit si on a assez de ses points et images avec une interpolation de lagrange. C'est le concept derrière le partage de clé secrète de Shamir.

Pour la théorie, on va dessiner une courbe qui va passer par un point grace à une équation, reproduire ca pour tous les points soumis et multiplier toutes les equations, voici à quoi ressemble l'équation :

\[ l_{i}(X) = \prod_{j=0,j\neq i}^{n} \frac{X - x_{j}}{x_{i} - x_{j}} \ ... \ \frac{X - x_{0}}{x_{i} - x_{0}} \frac{X - x_{1}}{x_{i} - x_{1}} \ ... \ \frac{X - x_{n}}{x_{i} - x_{n}} \]

Le serveur nous envoie 23 points et on peut essayer de reconstruire le polynome avec ces derniers :

from pwn import remote

host = 'crypto.heroctf.fr'
port = 9000

conn = remote(host, port)

data = conn.recvuntilS('>').decode()
given_points = eval(data.split('\n')[0])

F = FiniteField(2**256 - 189)
R = PolynomialRing(F, "x")

interp = R.lagrange_polynomial(given_points)
coefs = interp.coefficients()

print(coefs)
print(interp)

Spoiler : on obtient pas le bon polynome.

J'ai testé en local avec un flag du meme format que le flag utilisé dans le challenge. J'ai généré le polynome à partir du flag et un autre polynome par interpolation et ils ne correspondent pas.

L'explication c'est que je ne génère pas le polynome avec assez de points. J'en utilise 23 qui me génère 23 coefficients alors que le polynome de base en a 24 (pour calculer ca il suffit de calculer la longueur de la liste que génère C(FLAG)). Cependant je peux en calculer un de plus.

Lorsque le polynome est généré avec f = R(C(FLAG)), une liste de int est génrée avec C(FLAG). Puis le polynome est généré à partir de cette liste. Sauf que le premier élément de la liste sera converti en un coefficient avec x à la puissance 0 : $ a_{0}X^{0} = a_{0} $. C'est à dire : points[0] devient $ a_{0}X $ et points[1] devient $ a_{1}X^{1} $ ...

Par exemple avec une liste de points : [7, 4 ,3] on aura ce polynome : $ 3X^{2} + 4X^{1} + 7 $. Et donc, calculer le polynome pour x = 0 revient à faire 3*0 + 4*0 + 7 = 7.

Il se retrouve que le premier coefficient est généré avec les quatre premiers caractères du flag : Hero et representera la variable $ a_{0} $. Donc calculer $ f(0) $ donne le coefficient $ a_{0} $

On calule a0 ainsi :

from sage.all import *

F = FiniteField(2**256 - 189)
R = PolynomialRing(F, "x")
H = lambda n: int(hashlib.sha256(n).hexdigest(), 16)

known_coefficient = H('Hero') #51862623363251592162508517414206794722184767070638202339849823866691337237984

On peut donc ajouter ce point à la liste de point given_points.append([0, known_coefficient]).

Et on regenère la liste comme précédemment et on obtient le bon polynome :

91356407137791927144958613770622174607926961061379368852376771002781151613901*x^23 + 58688474918974956495962699109478986243962548972465028067725936901754910032197*x^22 + 71177914266346294875020009514904614231152252028035180341047573071890295627281*x^21 + [...] + 51862623363251592162508517414206794722184767070638202339849823866691337237984

Maintenant qu'on a le polynome, on va essayer de retrouver leur valeur en texte, c'est à dire avant d'avoir été haché en sha256.

La vulnérabilité résidait dans le fait qu'on puisse calculer un point supplémentaire.

Une autre solution proposée par cryptanalyse est de requeter le serveur plein de fois jusqu'à avoir suffisament de points pour reconstruire le polynome.

Récupération du flag

Ici la vulnérabilité est que on a des morceaux de 4 caractères et un jeu de caractères réduit donc les solutions sont réduites.

On sait que les coefficients sont générés avec des morceaux de quatres caractères de ce jeu de caractères : "abcdefghijklmnopqrstuvwxyzABCDEFGHIJKLMNOPQRSTUVWXYZ0123456789_{}" (j'ai ajouté les accolades). Ce qui nous fait un total de $ 65 ^{4} = 17850625 $ possibilités (bruteforcable).

On va générer un dictionnaire de correspondances valeur en int:plaintext et voir si ca correspond à des caractères de notre liste de coefficients qu'on a récupéré:

charset = bytes(string.ascii_letters + string.digits + '_{}')
candidate_list = list(itertools.product(charset, repeat=4))
candidate_list = ["".join(v).encode() for v in candidate_list]

rainbow_table = {}

print(f'Building the rainbow table with {len(candidate_list} entries !')

for candidate in candidate_list:
    int_hash = H(candidate)
    rainbow_table[int_hash] = candidate

# it tooks 15 seconds to build the table

assert rainbow_table[H(b'test')] == b'test'

flag_parts = [0] * len(flag_coefficients)

print("Looking up values in the rainbow table")

for coef in rainbow_table:
    if coef in flag_coefficients:
        flag_parts[flag_coefficients.index(H(b'Hero'))] = rainbow_table[coef]

Ca a pris 20 - 30 secondes en tout

Solve final

import hashlib
import re
import string
import requests
import itertools

from pwn import remote, context
from sage.all import *

host = 'crypto.heroctf.fr'
port = 9000

conn = remote(host, port)

data = conn.recvuntilS('>').decode()
given_points = eval(data.split('\n')[0])

F = FiniteField(2**256 - 189)
R = PolynomialRing(F, "x")
H = lambda n: int(hashlib.sha256(n).hexdigest(), 16)

known_coefficient = H('Hero') # 51862623363251592162508517414206794722184767070638202339849823866691337237984
given_points.append([0, known_coefficient])

interp = R.lagrange_polynomial(given_points)
flag_coefficients = interp.coefficients()


charset = bytes(string.ascii_letters + string.digits + '_{}')
candidate_list = list(itertools.product(charset, repeat=4))
candidate_list = ["".join(v).encode() for v in candidate_list]

rainbow_table = {}

print(f'Building the rainbow table with {len(candidate_list} entries !')

for candidate in candidate_list:
    int_hash = H(candidate)
    rainbow_table[int_hash] = candidate

assert rainbow_table[H(b'test')] == b'test'

flag_parts = [0] * len(flag_coefficients)

print("Looking up values in the rainbow table")

for coef in rainbow_table:
    if coef in flag_coefficients:
        flag_parts[flag_coefficients.index(H(b'Hero'))] = rainbow_table[coef]

flag = "".join(flag_parts)
print("Flag : {flag}")

FLAG : Hero{th3r3_4r3_tw0_typ35...}

Retex

Le challenge était facile à comprendre après avoir lu rapidement de la doc, on comprends aisément où chercher. J'ai pu mieux comprendre les l'interpolation de lagrange et les polynomes.

Liens utiles

http://exo7.emath.fr/cours/ch_polynomes.pdf
https://www.youtube.com/watch?v=nvkX1Bd90Gk
https://fr.wikipedia.org/wiki/Interpolation_lagrangienne
https://en.wikipedia.org/wiki/Modular_arithmetic
https://en.wikipedia.org/wiki/Shamir%27s_secret_sharing
https://doc.sagemath.org/html/en/reference/polynomial_rings/sage/rings/polynomial/polynomial_ring.html